构建图定义
| 变量 | 说明 |
|---|---|
| LinkID | 有向边索引 |
| SourceID | 有向边的起始顶点索引 |
| DestinationID | 有向边的终止顶点索引 |
| Cost | 有向边权重 |
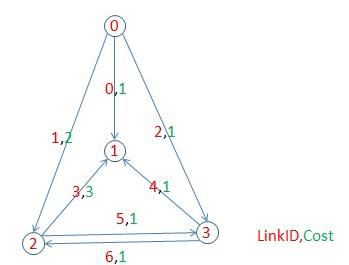
上图的信息表示为
0,0,1,1
1,0,2,2
2,0,3,1
3,2,1,3
4,3,1,1
5,2,3,1
6,3,2,1
拓扑排序
拓扑排序,其实就是寻找一个输入为0的顶点,该顶点是拓扑排序的第一个顶点。然后,将该顶点标记为删除;然后将与之相邻的顶点的入度减1,再继续寻找入度为0的顶点,直至所有的顶点都已经标记为删除或图中有环为止。
一种方式是遍历整个图中的顶点,寻找入度为0的顶点,然后将其删除,并更新相关顶点的入度。因此时间复杂度为o(v^2)
由于删除入度为0的顶点,只会更新与它相邻的顶点的入度,因此改进的方式是,先将入度为0的顶点放在栈或队列中。当队列不为空时,删除一个顶点,并更新与之相邻的顶点的入度。如果有一个顶点入度将为0,则将其加入队列。此时,拓扑排序的顺序就是顶点出列的顺序。时间复杂度为O(V+E)
拓扑排序实现
第1步,遍历图中的所有顶点,将入度为0的顶点加入队列;
第2步,从队列中删除一个顶点,打印顶点,并更新该顶点的邻接点的入度;如果邻接点的入度减1变为0,则加入队列
第3步,执行第2步,直到队列为空
public void topoSort() throws Exception{
int count = 0;//判断是否所有的顶点都出队了,若有顶点未入队(组成环的顶点),则这些顶点肯定不会出队
Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
//扫描所有的顶点,将入度为0的顶点入队列
Collection<Vertex> vertexs = directedGraph.values();
for (Vertex vertex : vertexs)
if(vertex.inDegree == 0)
queue.offer(vertex);
//度为0的顶点出队列并且更新它的邻接点的入度
while(!queue.isEmpty()){
Vertex v = queue.poll();
System.out.print(v.vertexLabel + " ");//输出拓扑排序的顺序
count++;
for (Edge e : v.adjEdges)
if(--e.endVertex.inDegree == 0)
queue.offer(e.endVertex);
}
if(count != directedGraph.size())
throw new Exception("Graph has circle");
}